stardate 20231119
No, I still do not really blog. However, twice with in the span of 4 weeks, I saw the same puzzle pop up. Once on Hacker News with a neat let’s make a solution using Sympy as a solver and once, well, in typical newspaper fashion.
This is the oft used form:
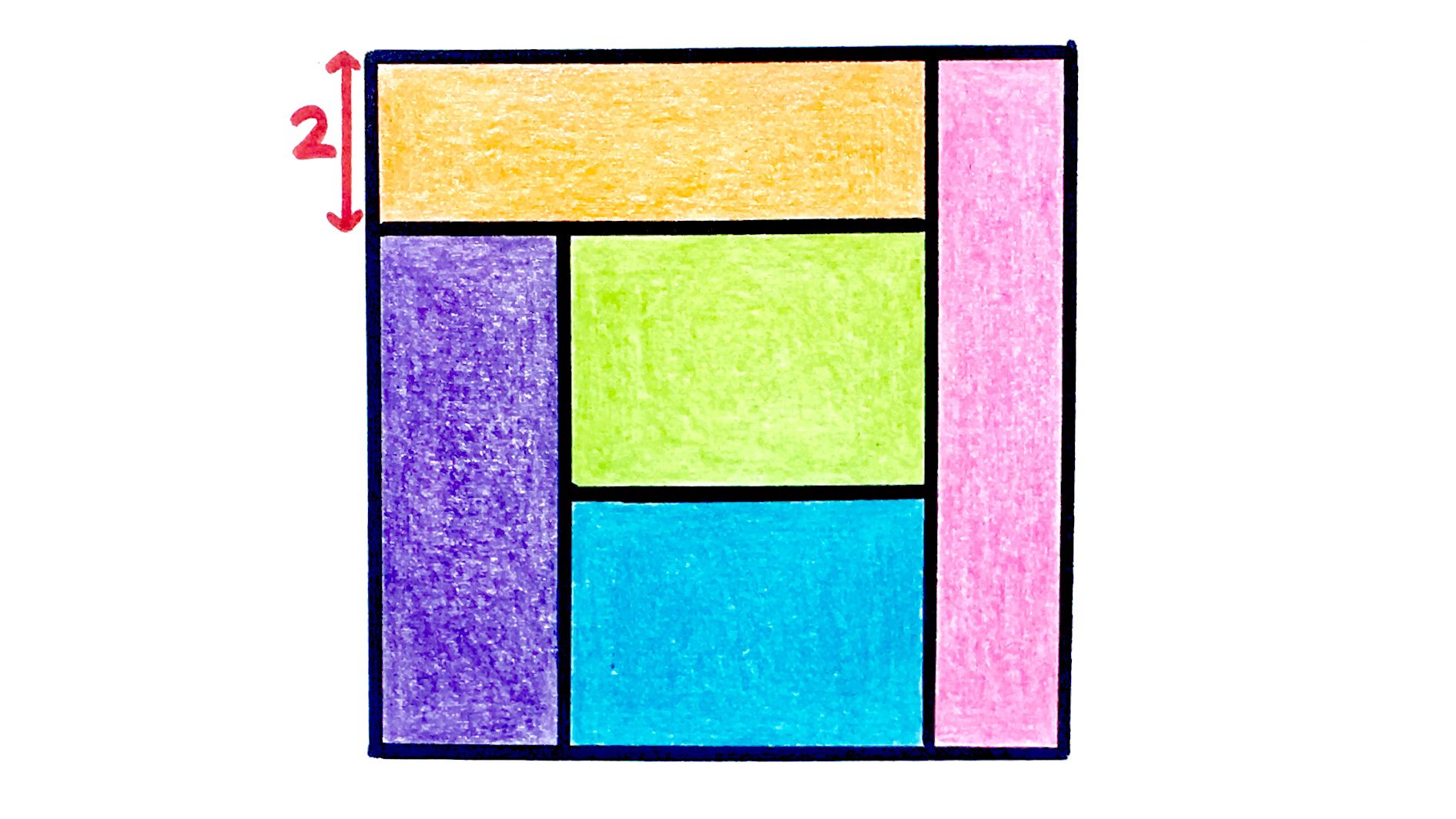
It’s the old, given the length one side, all areas within the square are of equal area, find the area of the square. SO? So? Well, the example with 5 equal areas, which illustrates a basic algebraic problem solving task, because of it’s dimensions is not SATISFYING!
Why? Well, since it’s designed with fractional widths and heights, you can easily find the area of the containing square, but the rest is, well, just fractions.
My version has 8 divisions. What’s the area? 6 being the left bottommost rectangle’s dimension, ‘a’ being it’s other: 3(6a) = c * a. 18a = ca. c=18. c+6=24. Area = 576. Ok. And then?

Well, usually this is the frustrating thing with the 5 equal sqaures division. You’re finished. Well, you can do the math, but it’s all fractions. Sigh.
So, I sat down an drew the same puzzle with, for my taste, more pleasing dimensions. My contrivance asks, ok, can you find all the sides?
Well, we can, by twos :). It’s simple once we know that 576 being the area, dividing by 8 square gives us 72 units.
So we can just plugin, beginning on the bottom left corner: 72/6 = 12, 72/18 = 4. Our bottom right rectangle is 8 high (12-4) and so it’s width (72/8) is 9. The topmost 3 rectangles are 3(x) = 24. in length. Since all have the same height, must be 8. Ok. NOW I’m done.
Now you can calculate all the dimensions of all the areas in you head and feel like you’ve accomplished something :) Was it worth the effort? I think so. But' I’m probably mad.
Now, onto: Boltyanskii, V., Hilbert’s Third Problem, Wiley, New York, 1978. Boltyanskii, V., Equivalent and Equidecomposable Figures, D. C. Heath, Boston, 1963. Frederickson, G., Dissections: Plane and Fancy, Cambridge U. Press, New York, 1997.